이 글에서는 기계학습(ML)에 대한 간단한 소개, 회귀(regressio)에 대한 개념 설명, 선형회귀에 대한 소개를 다룬다.



INTRO. 머신러닝 간단한 소개 

머신러닝. 우리말로 하면 기계학습. 거창하게 들리지만 그렇게 거창하지 않다.

머신러닝에는 학습 데이터가 존재하는 지도학습과 존재하지 않는 비지도학습이 있다. 지도학습은 선형대수학을 이용해 학습 데이터에 존재하는 독립변수(Independent Variables)와 종속변수(Dependent Variable)간 관계를 가장 잘 설명하는 모델을 만드는 것이다.

그렇다면 이 모델을 왜 만들까. 독립변수와 종속변수가 모두 있는 학습 데이터가 아닌 실제 데이터에서 종속 변수를 예측하기 위해서다. 실제 데이터는 독립변수(들)만 존재하는 데이터로 unseen data라고 한다.

지도학습은 종속변수의 종류에 따라 회귀 문제와 분류 문제로 나눌 수 있다. 종속변수가 연속형이라면 회귀 문제이고, 카테고리형 혹은 명목형이라면 분류 문제다.

(분류 작업에서 모델은 한 부류와 다른 부류를 분리하는 결정 경계를 찾고, 회귀 작업에서 모델은 입력-출력 관계에 맞는 함수를 근사한다. 분류는 회귀의 부분집합니다.)

회귀 문제를 풀기위해 사용되는 알고리즘이 '선형회귀(Linear regression)'다. 머신러닝에 입문할 때 가장 먼저 배우는 것이다.

범주형(categorical) 변수에 명목형(nominal)이 포함됨. 
범주형 변수에 명목형과 서열 변수가 있음.



선형회귀란? 


선형회귀 모델은 독립변수가 연속변수인 데이터를 가지고 최적의 파라미터를 찾아 독립변수(들)과 종속변수간 관계를 설명한다. 예를 들어, 독립변수 '경력'을 가지고 종속변수 '연봉'을 예측하는 선형회귀 모델을 만들 수 있다. 선형회귀 모델에서 파라미터 갯수는 독립변수의 갯수 + 1 (절편)와 같다. 예를 들어, 독립변수가 13개인 문제를 풀기 위한 선형회귀 모델의 파라미터는 14개다.

이때 파라미터 값들, 즉 회귀 계수들은  '선형(linear)'이어야 한다. 1차 다항식 형태를 띈다는 얘기! 독립변수 자체는 비선형이어도 된다. 



성능이 좋은 선형회귀 모델을 만들기 위해서는 IVs-DV를 가장 잘 설명할 수 있는 최적의 파라미터(회귀 계수) 값을 찾아야 한다. 이는 오차(실제 값 -모델을 통해 예측한 값)의 총합을 뜻하는 '비용함수(a function of the parameters)'를 최소화하는 값으로 찾으면 된다.

선형회귀는 독립변수 및 종속변수의 수에 따라 다음과 같이 나뉜다. 

  • 단순 선형 회귀 
  • 다중 선형 회귀 : 독립 변수가 여러 개. 파라미터의 절대값이 클수록 해당 독립 변수가 종속 변수에 대해 갖는 영향력이 크다고 해석할 수 있다.
  • 다변량 선형 회귀 : 독립 변수가 둘 이상의 종속 변수에 영향을 주는 경우. 




최적의 파라미터를 찾기 = 비용함수를 최소로 하는 값 찾기 


비용함수에는 MAE(mean absolute errors)와 MSE(mean squared errors) 등 두 종류가 있다. 절대값을 계산하는 것보다 제곱 계산이 더 쉬워 MSE가 더 많이 사용된다.

MSE의 최소값을 찾아야 하는데, 그러기 위해서는 MSE를 계산해야 한다. 계산 방법에는 두 가지가 있다.

1차 도함수(FOC, First order condition)을 이용한 Normal equation method와 경사하강법(Gradient descent method)이다. Normal equation method는 선형회귀 모델에서만 사용된다.




- Normal Equation Method


Normal Equation Method는 비용함수가 convex할 때 사용된다. 



잠깐, convex?

출처: 블로그 '꿈을 위한 단상'



- Gradient Descent (경사 하강법) 

경사 하강법은 비용함수가 convex하지 않을 때 사용한다. Normal Equation Method와 달리 딥러닝에서도 많이 사용되는 방법이다.



처음 시작점을 랜덤하게 정해, 시작점에서부터 미세하게 자리를 옮겨가며 기울기를 조금씩 조절하며 비용함수의 최저점을 찾는다.



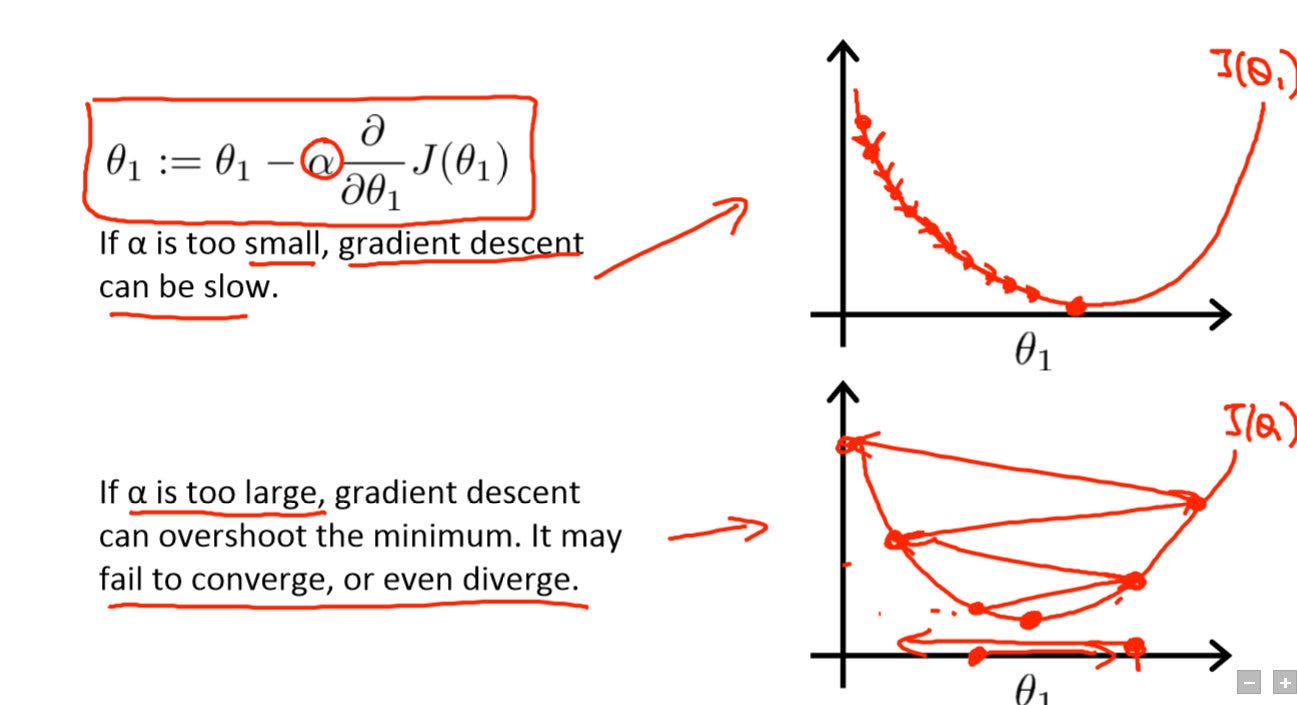
이때 하이퍼 파라미터는 에타 (learning rate 혹은 step strength)를 너무 크게 설정하면 핑퐁을 치다 발산하고, 너무 작으면 최저점을 찾는 데 너무 오랜 시간이 걸린다.
 
Image for post
source : Pavel Surmenok's Medium



경사 하강법은 업데이트 할 때 학습 데이터에서 사용하는 데이터 포인트의 수에 따라 다시 세 가지로 나뉜다. 

(1) Batch GD

 : 학습 데이터의 모든 관측치 정보를 사용해, 한 번 업데이트 한다. 시간이 오래 걸린다.

(2) Stochastic GD (SGD) 

: 학습 데이터에서 데이터 포인트 (관측치) 하나를 랜덤하게 선택해 업데이트한다. 계산이 빠르지만, 랜덤하게 뽑은 데이터 포인트가 아웃라이어일수록 .. 핑퐁 문제가 발생할 가능성이 높다. 

(3) Mini-batch GD 

: (1) & (2)의 혼종으로, 가장 많이 사용된다. 업데이트 한 번에 사용되는 데이터 포인트의 수 h는 1 < h < N (총 데이터 포인트의 수) 

대부분의 경우, 독립변수들의 값을 normalization한 후 경사 하강법을 적용한다.