1. K-means
- 군집화를 하는 비지도 학습 방법
- 유클리디안 방법을 사용
- 군집의 갯수인 K는 하이퍼 파라미터이고, 최적의 K를 찾는 게 관건
How it works
1) K = 3이면, 데이터 포인트들을 3개 그룹으로 나눈다는 의미다. 각 그룹의 중심이 되는 벡터는 처음에 '임의'로 선택된다.
2) 모든 벡터를 3개의 중심이 되는 벡터 중 가장 가까운 벡터가 속한 그룹에 할당 (이때 유클리디안 거리 사용)
이때, 분할된 공간의 경계면을 Voronoi partition이라고 한다.
3) 이제 중심 벡터를 업데이트 해줘야 한다. 어떻게? 같은 그룹에 속하는 점들의 평균값을 새로운 중심 벡터로 삼는다! (이 새로운 중심점은 가상의 중심점)
2~3을 반복하는데 무한히 반복할 수 없으니, 과정을 거치며 다른 그룹에 할당되는 점이 없을 때까지 계속하거나, 혹은 몇 번 반복할지 정할 수도 있다.
How to find an Optimal K
일단, domain knowledge가 있어야 함. 이외에 사용할 수 있는 두 가지 방법이 있음
1. Elbow method
 |
| 갓상엽 쌤 |
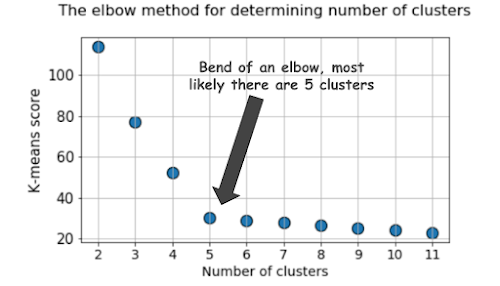 |
| optimal K = 5 source : kdnuggets |
2. Silhouette score
a : 해당 데이터 포인트가 속한 군집의 다른 포인트들과의 평균 거리
b: 해당 데이터 포인트의 next best cluster에 속한 포인트들과
b - a를 max(a, b)로 normalize 해준 값이 Silhouette score
-1 < Silhouette score < 1
1에 가까울수록 Optimal K다.
 |
| source : Orange |
2. Hierarchical Clustering
Hierarchical clustering 방법은 스텝 바이 스텝 방식으로 데이터 포인트들을 군집화하는 방식이다.
일단 데이터 포인트들을 벡터로 변환해 특정 차원의 공간에 위치시킨다.
이제 2가지 방법으로 Hierarchical Clustering을 할 수 있다.
(1) Bottom-up approach : 가장 가까운 군집들을 순차적으로 연결해 일단 하나의 커다란 군집을 생성하는 방법이다. Agglomerative 방법이라고도 하는데, 일반적으로 사용되는 방법이다!
(2) Top-down approach : 일단 모든 데이터 포인트들이 하나의 커다란 군집에 속한다고 가정하고, 순차적으로 연결을 끊어 모든 데이터 포인트들을 분리하는 방법이다. Divisive 방법이라고도 한다.
Agglomerative Hierarchical clustering이 많이 사용되므로, 이 방법을 설명한다.
군집화를 처음 시작할 때 각 데이터 포인트를 하나의 군집으로 간주한다. 즉, 처음에는 number of data point = number of cluster이다. 데이터 포인트, 즉 클러스터가 n개 있다고 하자.
이제 가까운 군집끼리 서로 묶어나가는 방식으로 n을 줄여나간다. n=1이 돼 클러스터가 하나가 될 때까지 반복한다.
가깡누 군집끼리 서로 묶기 위해서는 두 군집 간 거리를 계산해야 한다. 계산 방법에는 4가지가 있다.
(1) single : 각 클러스터를 구성하는 데이터 포인트 중에서 가장 가까운 데이터 포인트 간의 거리를 사용
(2) complete : single의 반대. 즉, 가장 먼 데이터 포인트 간의 거리를 사용
(3) average : 각 클러스터를 구성하는 데이터 포인트들 간의 평균 거리
(4) ward : 두 개의 클러스터가 합쳐졌을 때의 데이터 포인트들이 갖는 '분산'이 가장 작은 클러스터끼리 묶어주는 방법
Practice with Kaggle data

1 Comments
hiararchical 단점 : 데이터가 크면 안 돌아감.
ReplyDeletePost a Comment